4 Linear Mixed Models

4.1 ANOVA with random factors

The simplest linear mixed models are used to analyze linear models for one-way ANOVA, randomized complete block designs, and two-way ANOVA. Mixed models as opposed to fixed models (the linear models you have heretofore studied) are needed when factors have levels that are random. Random levels occur whenever the units making up those levels behave like random samples from a population. Two examples are given below. And, we discuss how to perform ANOVA-like tests for factors that are random rather than fixed. The upshot is that (at least for balanced experiments/datasets) the tests for fixed effects are identical to those for random effects, only the interpretation is different (and importantly so!).

4.1.1 Strength of metallic bonds

The dataset below, called “Bonds”, contains responses for 21 samples of metals, 7 each for iron, nickel, and copper, that quantify the strength of metallic bonds. One sample from each metal was extracted from each of 7 ingots. We expect ingots to act like blocks—differences in ingots account for a substantial amount of variability in the responses, but the precise block effects are of no inferential/scientific inference. We only include the blocks in order to reduce the residual variance after accounting for block variance. A randomized controlled block design describes how this data was collected, but, if we repeated the experiment, the blocks (ingots) would be completely different. That is, the blocks are not fixed but random. Rather than estimating block effects that would surely change experiment to experiment, we should focus on estimating the amount of variability explained by the blocks, which should remain about the same experiment to experiment. This suggests a different model than used to analyze RCBD experiments with fixed blocks.

The usual linear model for fixed blocks is \[y_{ijk} = \mu + \alpha_i + \beta_j + \epsilon_{ij},\] where \(y_{ij}\) is the response for treatment (metal) \(i\) in block (ingot) \(j\); the \(\alpha_i\)’s are the metal (treatment) effects; the \(\beta_j\)’s are the ingot (block) effects; and, \(\epsilon_{ij}\stackrel{iid}{\sim}N(0,\sigma^2)\) are the random residuals.

The above linear model is the wrong model for this data because the block effects (and, hence, also the interaction effects) are meaningless outside of the given data set; these are not population-level parameters because the blocks are random rather than fixed. The appropriate model (given normality and independence of random residuals is reasonable) is the following mixed effects model:

\[\begin{equation} y_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}, \tag{4.1} \end{equation}\] where \(\beta_j\stackrel{iid}{\sim}N(0, \sigma_b^2)\) and, independently, \(\epsilon_{ij}\stackrel{iid}{\sim}N(0,\sigma^2)\).

For balanced experiments (the number of replicates is equal across each combination of factor levels) we can test for block and treatment effects by comparing nested/aggregated models. Let \(\overline Y_{i\cdot}\) denote the mean response for metal \(i\) averaged over ingots. We can write down the following aggregated model from (4.1) as \[\begin{equation} \overline y_{i\cdot} = \mu + \alpha_i + \epsilon_{i}, \tag{4.2} \end{equation}\] where \(\epsilon_i = \frac{1}{J}\sum_{j=1}^j \epsilon_{ij}\). Then, \(\epsilon_j\) has variance \(\sigma_b^2 + \sigma^2/J\). The F statistic \[F = \frac{J\cdot MSE_{agg}}{MSE_{full}}\] where \(MSE_{agg}\) and \(MSE_{full}\) are the mean squared errors from the models in (4.2) and (4.1) can be used to test the hypothesis \(H_0:\sigma_b^2 = 0\).

4.1.2 Machine productivity

The dataset given below contains the results of a designed experiment to evaluate worker productivity using 3 different industrial machines. The goal is to determine which machine is most productive while controlling for natural variation in worker productivity. The observed workers represent a random sample from a population of workers (blocks), analogous to the ingots in the previous example. The difference between the two examples (besides the context) is that the machine treatments are replicated wihtin workers, so that there are three observations of a productivity score fore each worker for each type of machine. This means that we can fit a model with interaction terms capable of capturing changes in machine effects on productivity between different workers (if those changes are present): \[\begin{equation} y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk}, \tag{4.3} \end{equation}\] where \(k\) denotes the \(k^{\text{th}}\) replicate within machine \(i\) and worker \(j\); and where \((\alpha\beta)_{ij}\) denote the machine-worker interaction effects.

Let \(\overline Y_{ij\cdot}\) be the mean response averaging over replicates for the treatment \(i\) and block \(j\) combination. Then, \[\begin{align*} V(\overline Y_{ij\cdot}) &= V\left(K^{-1}\sum_{k=1}^K Y_{ijk}\right) \\ &= \frac{1}{K^2}V\left(\sum_{k=1}^K \{\mu+\alpha_i+\beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk}\}\right)\\ & = \frac{1}{K^2}V\left(K\mu + K\alpha_i + K\beta_j + K(\alpha\beta)_{ij} + \sum_{k=1}^K \epsilon_{ijk}\right)\\ & = \sigma_b^2 + \sigma_{ab}^2 + K^{-1}\sigma^2. \end{align*}\] If we rewrite the model for the cell mean responses as \[\begin{equation} \overline y_{ij\cdot} = \mu + \alpha_i + \beta_j + \epsilon_{ij}, \tag{4.4} \end{equation}\] then the aggregated error term follows \(\epsilon_{ij}\stackrel{iid}{\sim}N(0, \sigma_{ab}^2 + \sigma^2/K)\). The residual mean square (or called the mean squared error) of model (4.3) (let’s call it \(MSE_{\text{full}}\)) has mean \(\sigma^2\) with \(n-p_1\) degrees of freedom where \(n\) is the sample size and \(p\) is the number of coefficients in the fitted model (\(p_1\) equals the number of crossed factor levels, the number of blocks times the number of treatments). The residual mean square for the aggregated model in (4.4) (let’s call it \(MSE_{\text{agg}}\)) has mean \(\sigma_{ab}^2 + \sigma^2/K\) with \(n/K-p_2\) degrees of freedom where \(p_2\) is the number of treatments plus the number of blocks minus 1. An unbiased estimate of \(\sigma_{ab}^2\) is given by \(MSE_{\text{agg}} - \frac{1}{K}MSE_{\text{full}}\). Consider testing the null hypothesis \(H_0:\sigma_{ab}^2 = 0\). The statistic \[F := \frac{K\cdot MSE_{agg}}{MSE_{full}}\stackrel{H_0}{\sim}F_{n/K-p_2, n-p_1},\] that is, under the null hypothesis. The test that rejects \(H_0\) for \(F > F_{1-\alpha,n/K-p_2, n-p_1}\) is exactly equivalent to the partial F test between the full model and the full model without the interaction terms (the additive model).

Below we use R to compute ANOVA tables for the full model, full model without interaction, and the aggregated model. The F test statistic for the aggregated model is about 46.13 on 10 and 36 degrees of freedom, which exactly matches the partial F test between the full and additive models.

library(nlme)

# aggregated model
Mach.agg <- aggregate(score~Machine*Worker, data = Machines, FUN=mean)

m2 <- lm(score~Machine+Worker, data = Mach.agg)

anova(m2)

## Analysis of Variance Table
## 
## Response: score
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## Machine    2 585.09 292.544 20.5761 0.0002855 ***
## Worker     5 413.97  82.793  5.8232 0.0089495 ** 
## Residuals 10 142.18  14.218                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# full model with interaction
m0 <- lm(score~Machine*Worker, data = Machines)

anova(m0)

## Analysis of Variance Table
## 
## Response: score
##                Df  Sum Sq Mean Sq F value    Pr(>F)    
## Machine         2 1755.26  877.63  949.17 < 2.2e-16 ***
## Worker          5 1241.89  248.38  268.63 < 2.2e-16 ***
## Machine:Worker 10  426.53   42.65   46.13 < 2.2e-16 ***
## Residuals      36   33.29    0.92                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(142.18*3/10)/(33.29/36)

## [1] 46.12628

1-pf((142.18*3/10)/(33.29/36), 10, 36)

## [1] 0

# additive model (no interaction)
m1 <- lm(score~Machine+Worker, data = Machines)

anova(m1)

## Analysis of Variance Table
## 
## Response: score
##           Df  Sum Sq Mean Sq F value    Pr(>F)    
## Machine    2 1755.26  877.63  87.798 < 2.2e-16 ***
## Worker     5 1241.89  248.38  24.848 4.867e-12 ***
## Residuals 46  459.82   10.00                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

anova(m1,m0)

## Analysis of Variance Table
## 
## Model 1: score ~ Machine + Worker
## Model 2: score ~ Machine * Worker
##   Res.Df    RSS Df Sum of Sq     F    Pr(>F)    
## 1     46 459.82                                 
## 2     36  33.29 10    426.53 46.13 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

4.2 A general linear mixed model

For experiments comparing responses between factors the ANOVA-type analyses above are sufficient. But, for more general models with random effects, e.g., those including continuous covariates, general-purpose methods are needed. The general mixed effects model may be written \[Y = X\beta+ Z\alpha + \epsilon\] where Y is an \(n\times 1\) response, \(X\) is an \(n \times p\) design matrix for fixed (non-random) effects; \(Z\) is and \(n\times a\) matrix for random effects; \(\beta\) is a \(p\times 1\) non-random coefficient vector; \(\alpha\sim N_a(0, \psi_\theta)\) is an \(a\times 1\) multivariate normal random coefficient vector with mean 0 and covariance matrix \(\psi_\theta\) indexed by a parameter \(\theta\); and \(\epsilon\sim N_n(0, \Lambda_\theta)\) is a multivariate normal random residual vector with covariance matrix \(\Lambda_\theta\). An alternative way of writing the model (quite succintly) is \[\begin{equation} \tag{4.5} Y\sim N_n(X\beta, Z \psi_\theta Z^\top + \Lambda_\theta). \end{equation}\] For abbreviation we will denote \(\Sigma = Z \psi_\theta Z^\top + \Lambda_\theta\) and we will often drop \(\theta\) from \(\psi\) and \(\Lambda\) to save pixels.
### Parameter estimation using PML

The linear mixed model in (4.5) may be fit using maximum likelihood estimation (MLE), but the (potentially) complicated covariance structure poses challenges to numerical maximization of the likelihood function. Rather than straightforward MLE, linear mixed models are usually fit using either restricted maximum likelihood estimation (REML, also called residual MLE) or profile maximum likelihood estimation (PML). Both approaches aim to simplify the computation of the maximum while retaining the good asymptotic properties of maximum likelihood estimators. While MLE is a frequentist concept, it turns out that REML can be derived most intuitively using a Bayesian approach.

If you have previously covered general linear models, i.e., \(Y = X\beta + \epsilon\) where \(Cov(\epsilon) = W\) for some known \(W\) or equals \(\sigma^2 W\) for an unknown scalar \(\sigma^2\) and a known matrix \(W\), then you are familiar with weighted least squares (WLS) estimation. Often weighted least squares is employed in response to observed heteroskedasticity in residuals related to covariates so that \(W\) depends on covariate values. If the linear mixed model covariance parameter \(\theta\) were known, then the model could be fit using WLS: \[\hat\beta(\theta) = (X^\top \Sigma^{-1}X)^{-1}X^\top \Sigma^{-1}Y\] just as in other applications of weighted least squares.

The above WLS solution inspires the PML technique: maximize the likelihood with respect to \(\theta\) after plugging in \(\beta = \hat\beta(\theta)\). PML reproduces MLEs exactly; its advantage is its simplified formulation of the likelihood maximization problem.

Nevertheless there are two problems with the PML strategy suggested above: one computational and the other statistical.

The first problem is that PML/WLS requires inverting the \(n\times n\) matrix \(\Sigma\). For even moderate sample sizes this matrix inversion can be both computationally demanding and computationally unstable. Fortunately, some clever linear algebra resolves this problem. Define matrix \(A:=\psi^{-1} + Z^\top \Lambda^{-1}Z\). Observe that the matrix \(\Lambda^{-1} - \Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1}\) equals the inverse of \(Z\psi Z^\top + \Lambda\): \[\begin{align*} &(\Lambda^{-1} - \Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1})(Z\psi Z^\top + \Lambda) \\ & = \Lambda^{-1}Z\psi Z^\top + I - \Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1}Z\psi Z^\top - \Lambda^{-1}ZA^{-1}Z^\top \\ & = I + \Lambda^{-1}Z(\psi - A^{-1}(Z^\top \Lambda^{-1}Z\psi + I))Z^\top \\ & = I+\Lambda^{-1}Z(\psi - \psi(Z^\top \Lambda^{-1}A\psi + I)^{-1}(Z^\top \Lambda^{-1}A\psi + I))Z^\top \\ & = I \end{align*}\] The key property of this inverse is that it only requires computing the inverse of \(p\times p\) and \(a\times a\) matrices, and does not require the computation of any \(n\times n\) matrix inverse. In many practical applications both \(p\) and \(a\) are much smaller than \(n\), and the matrices \(\Lambda\) and \(\psi\) often have simple/sparse structures with many exact zeroes, so that the above matrix inversions may be performed very quickly and reliably.

The second issue with PML cannot as easily be overcome. Think back to the Gauss-Markov model \(Y = X\beta+\epsilon\) where \(Cov(\epsilon) = \sigma^2 I_n\). Recall that the MLE \(\hat\sigma^2\) is biased, i.e., \(E(\hat\sigma^2) = \frac{n-p}{n}\sigma^2\). In practice we may have a substantial number of covariates relative to sample size so that this bias can be quite significant; and, importantly, the bias results in an underestimate which causes over-optimism with respect to inferences concerning \(\beta\). The same phenomenon occurs in ML/PML estimation: the PML estimate of \(\theta\) is biased. The desire for an estimation strategy that constructively produces less-biased estimates of covariance parameters is the motivation for REML, covered next.

4.2.1 REML - frequentist approach

There are two formulations both leading to the residual (also called restricted/reduced) maximum likelihood approach (REML), one frequentist (non-Bayesian) and the other Bayesian. Let’s explore both approaches.

The motivation for REML is to produce unbiased (or at least less biased than MLE) estimates of the covariance parameters. The REML approach to doing this may be interpreted as a likelihood approach based on residuals, or as a marginal likelihood approach to covariance parameter estimation.

Begin with the linear mixed model in (4.5). Assume \(X\) has full rank \(p\) and let \(L = [L_1 \,\,L_2]\) denote a block matrix of \(n\times p\) and \(n\times (n-p)\) blocks with the properties \[L_1^\top X = I_p \quad\text{and}\quad L_2^\top X = 0_{n-p},\] such that \(L\) has full rank \(n\).

This setup is a bit abstract, so it helps to find at least one concrete example of such an \(L\). Start with the projection matrix \(P_X := X(X^\top X)^{-1}X^\top\). Since \(P_X\) is a symmetric, idempotent matrix of rank \(p\) its eignevalues can only be zero or one, and, the number of eigenvalues (called multiplicity) of value one is equal to its rank, exactly \(p\). In addition, its eigenvectors are orthonormal. Hence, \[P_X = \begin{bmatrix}V_1 & V_2\\ V_3 &V_4\end{bmatrix}\begin{bmatrix}1_{p\times p} & 0_{p\times n-p}\\ 0_{n-p \times p} & 0_{n-p \times n-p}\end{bmatrix}\begin{bmatrix}V_1 & V_2\\ V_3 &V_4\end{bmatrix}^\top.\] It follows from this representation that \[P_X = \begin{bmatrix}V_1 \\ V_3\end{bmatrix}\begin{bmatrix}V_1 \\ V_3 \end{bmatrix}^\top=:L_1L_1^\top\] Furthermore, if \(v\) is an eigenvector of \(P_X\) with eigenvalue 1, then \(v\) is an eigenvector of \(I-P_X\) with eigenvalue 0 just by the definition of an eigenvalue (\(Av=\lambda v\)). It follows that \[I-P_X = \begin{bmatrix}V_2 \\ V_4\end{bmatrix}\begin{bmatrix}V_2 \\ V_4 \end{bmatrix}^\top=:L_2 L_2^\top.\] By construction, \(L_1L_2^\top = 0\), \(L_1^\top L_1 = I_p\) and \(L_2^\top L_2 = I_{n-p}\). The columns of \(L\) are orthogonal, and so \(L\) is full rank.

In what follows, note that the REML estimates are invariant to the choice of \(L\), so long as it has the above three properties.

Now, consider the full rank linear transformation \(Y \mapsto LY = [Y_1 \quad Y_2]^\top\). By the properties of \(L\), we have \[LY = \begin{bmatrix} Y_1\\Y_2 \end{bmatrix} \sim N\left(\begin{bmatrix} \beta \\ 0\end{bmatrix}, \begin{bmatrix} L_1^\top \Sigma L_1 &L_1^\top \Sigma L_2\\ L_2^\top \Sigma L_1 & L_2^\top \Sigma L_2 \end{bmatrix}\right)\] where \(\Sigma = Cov(Y) = Z \psi_\theta Z^\top + \Lambda_\theta\).

The next step is to consider an equivalent characterization of the distribution of \((Y_1, Y_2)\) as the product of the conditional distribution of \(Y_1|Y_2 = y_2\) and the marginal distribution of \(Y_2\). Using the general formulas for the conditional distribution of a multivariate normal random vector, we get \[Y_1|y_2 \sim N(\beta - L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1}y_2, \, L_1^\top \Sigma L_1-L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1} L_2^\top \Sigma L_1).\] Some tedious linear algebra (omitted here) can be used to show that the above covariance matrix is actually equal to \((X^\top \Sigma^{-1}X)^{-1}\), regardless of the specific choice of \(L\).

Therefore, the conditional likelihood is given by \[\ell_c := \text{const.} - \tfrac12\log |(X^\top \Sigma^{-1}X)^{-1}| -\tfrac{1}{2}(y_1 - \beta - y_2^\star)X^\top \Sigma^{-1}X(y_1 - \beta - y_2^\star)^\top, \] where \(y_2^\star = L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1}y_2\).

Again, some tedious linear algebra computations can be used to show that \[L_2(L_2^\top \Sigma L_2)^{-1}L_2^\top = \Sigma^{-1} - \Sigma^{-1}X(X^\top\Sigma^{-1} X)^{-1} X^\top\Sigma^{-1},\] which may be computed efficiently using the equivalent form of \(\Sigma^{-1}\) given above. Furthermore, the block matrix determinant identity given by \[det\begin{bmatrix}A & B\\ B^\top & C\end{bmatrix} = |C||A - B^\top C^{-1}B|,\] applied to \(L^\top\Sigma L\) can be used to show that \[\log |L_2^\top \Sigma L_2| = \log|L^\top\Sigma L| + \log |X^\top \Sigma^{-1}X|.\] Standard rules for determinants imply \[\log|L^\top\Sigma L| = \log|L^\top L\Sigma| = \log|L^\top L|+\log|\Sigma|.\] Using these simplified expressions, and noting that \(\log|L^\top L|\) is constant in parameters, we may write the marginal (or residual) likelihood as \[\ell_r:= \text{const}.-\tfrac12 \log |\Sigma| +\tfrac12 \log|X^\top \Sigma^{-1} X| -\tfrac12 y^\top(\Sigma^{-1} - \Sigma^{-1}X(X^\top\Sigma^{-1} X)^{-1} X^\top\Sigma^{-1})y.\]

What is the reason for referring to \(\ell_r\) as a residual loglikelihood? Recall \(\ell_r\) is the marginal loglikelihood of \(L_2^\top Y\) where \(L_2^\top X = 0\). Therefore, \[E(L_2^\top Y) = L_2^\top X\beta = (L_2^\top X)\beta = 0\beta = 0,\] which shows \(L_2^\top Y\) behaves like a residual vector.

The REML estimate of \(\theta\) is given by the maximizer of \(\ell_r\) with respect to \(\theta\). Note also that this is simply the MLE of \(\theta\) with respect to the marginal likelihood of \(L_2^\top Y\), i.e., the likelihood of “part of the data”.

Next, consider maximizing the conditional likelihood \(\ell_c\) with respect to \(\beta\) and where \(\theta=\hat\theta\) is fixed at its REML estimate, i.e., \(\Sigma = \hat\Sigma\). Take the first derivative with respect to \(\beta\), equate to zero, and observe \[\begin{align*} \hat\beta &= y_1 - L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1}y_2\\ &= L_1^\top y - L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1}L_2^\top y\\ &= L_1^\top \Sigma \Sigma^{-1}y - L_1^\top \Sigma L_2(L_2^\top \Sigma L_2)^{-1}L_2^\top \Sigma\Sigma^{-1}y\\ & = (L_1^\top \Sigma - (L_1^\top \Sigma L_2)(L_2^\top \Sigma L_2)^{-1}L_2^\top \Sigma)\Sigma^{-1}y\\ & = (L_1^\top \Sigma L_1^\top X - (L_1^\top \Sigma L_2)(L_2^\top \Sigma L_2)^{-1}L_2^\top \Sigma L_1^\top X)\Sigma^{-1}y\\ & = [(L_1^\top \Sigma L_1)-(L_1^\top \Sigma L_2)(L_2^\top \Sigma L_2)^{-1}(L_2^\top \Sigma L_1)]X\Sigma^{-1}y\\ & = (X^\top \Sigma^{-1}X)^{-1}X^\top \Sigma^{-1}y, \end{align*}\] using that \(L_1^\top X = I\) and the equivalence between the conditional covariance of \(Y_1|y_2\) and \((X^\top \Sigma^{-1}X)^{-1}\) shown above.

We conclude that the REML estimator of \(\beta\) is a weighted least squares estimator in which the weight matrix is given by the REML-based plug-in estimator \(\hat\Sigma^{-1}\).

4.2.2 REML - Bayesian approach

Suppose we model (in a Bayesian sense) the parameter \(\beta\) with an improper constant prior, and the random component \(\alpha\) with a multivariate normal prior with covariance \(\psi\). For whatever parameters define \(\theta\), endow those with constant/improper priors as well. Then, combining priors and multivariate normal likelihood we have the following posterior: \[\log\Pi_n(\beta) = \text{const.} - \tfrac12 \left(y - X\beta - Z\alpha\right)^\top \Lambda^{-1}\left(y - X\beta - Z\alpha\right) - \tfrac12\alpha^\top \psi^{-1}\alpha . \] A nice (but somewhat hard to find) factorization of the posterior is due to Searle et al. (Variance Components, Section 9.2). Expand the exponent: \[\begin{align*} \log\Pi_n(\beta) &= \text{const.} - \tfrac12 \left(y - X\beta\right)^\top \Lambda^{-1}\left(y - X\beta\right)\\ &-\tfrac12 \alpha^\top (\psi^{-1} + Z^\top \Lambda^{-1}Z)\alpha + \alpha^\top Z^\top \Lambda^{-1}(y - X\beta) \end{align*}\] Let \(A:=\psi^{-1} + Z^\top \Lambda^{-1}Z\) and complete the square in \(\alpha\): \[\begin{align*} \log\Pi_n(\beta) &= \text{const.} - \tfrac12 \left(y - X\beta\right)^\top \Lambda^{-1}\left(y - X\beta\right)\\ &-\tfrac12(\alpha - A^{-1}Z^\top\Lambda^{-1}(y-X\beta))^\top A(\alpha - A^{-1}Z^\top\Lambda^{-1}(y-X\beta))\\ &+\tfrac12(y-X\beta)^\top\Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1} (y-X\beta). \end{align*}\] Combine the terms quadratic in \(y-X\beta\). The resulting matrix \(\Lambda^{-1} - \Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1}\) is equal to \((Z\psi Z^\top + \Lambda)^{-1}\), which is a fact we used above in the frequentist approach to REML. Therefore, the posterior factorizes into \[\begin{equation} \tag{4.6} \begin{aligned} \log\Pi_n(\beta) &= \text{const.} - \tfrac12 \left(y - X\beta\right)^\top (Z\psi Z^\top +\Lambda)^{-1}(y - X\beta) \\ &- \tfrac12(\alpha - A^{-1}Z^\top\Lambda^{-1}(y-X\beta))^\top A(\alpha - A^{-1}Z^\top\Lambda^{-1}(y-X\beta)) \end{aligned} \end{equation}\]

Integrate over \(\alpha\) to obtain the posterior for \(\beta\). Marginally, \(\alpha\) is multivariate normal; therefore, we obtain \[\Pi_n(\beta) = (2\Pi)^{-n/2}|\Lambda|^{-1/2}|\psi|^{-1/2}|A|^{-1/2}\exp\left\{-\tfrac12 \left(y - X\beta\right)^\top (Z\psi Z^\top +\Lambda)^{-1}(y - X\beta)\right\}.\]

It can be verified that \(|Z\psi Z^\top +\Lambda| = |\Lambda||\psi||A|\) by using the following identity \[|D^{-1} - CA^{-1}B| = |D||A^{-1}||A - BD^{-1}C|\] where \(Z\psi Z^\top +\Lambda = D^{-1} - CA^{-1}B = (\Lambda^{-1} - \Lambda^{-1}ZA^{-1}Z^\top \Lambda^{-1})^{-1}\); and, see, e.g., Appendix M equation 31 in Searle et al. (Variance Components). As a result, the posterior for \(\beta\) is multivariate normal with covariance \(Z\psi Z^\top +\Lambda\).

In the exponent, add and subtract \(X\hat\beta = X(X^\top \Sigma^{-1} X)^{-1}X^\top \Sigma^{-1}y\) (which depends on \(\theta\)) in the quadratic to obtain \[\begin{align*} \left(y - X\beta\right)^\top \Sigma^{-1}(y - X\beta) & = \left(y - X\hat\beta\right)^\top \Sigma^{-1}(y - X\hat\beta)\\ & -2 \left(y - X\hat\beta\right)^\top \Sigma^{-1}(X\hat\beta - X\beta)\\ & + \left(X\hat\beta - X\beta\right)^\top \Sigma^{-1}(X\hat\beta - X\beta). \end{align*}\] It is straightforward to show the middle term is zero. Therefore, the joint posterior for \((\beta, \theta)\) may be written \[\log \Pi_n(\beta, \theta) = \text{const}. -\tfrac12\log|\Sigma|-\tfrac12(y-X\hat\beta)^\top \Sigma^{-1}(y-X\hat\beta) -\tfrac12(X\hat\beta - X\beta)\Sigma^{-1}(X\hat\beta - X\beta)\]

If we integrate out \(\beta\) (w.r.t. a multivariate normal density), then we obtain the following marginal posterior for the variance parameters: \[\log\Pi_n(\theta) = \text{const.} - \tfrac{1}{2}\log|\Sigma| + \tfrac{1}{2}\log|X^\top \Sigma^{-1}X|-\tfrac12 \left(y - X\hat\beta\right)^\top \Sigma^{-1}(y - X\hat\beta).\]

4.2.3 Predicting random effects and responses

If we set \(\beta = \hat\beta\) in (4.6) we see that the distribution of \(\alpha|\beta = \hat\beta\) is multivariate normal with mean (and mode) equal to \(A^{-1}Z^\top\Lambda^{-1}(y-X\hat\beta)\). This quantity is the predictor \(\hat\alpha\) of \(\alpha\) when \(\beta\) is set to the REML estimator, and it has a clear Bayesian interpretation as a posterior mean and maximum a posteriori point estimate.

The best linear unbiased predictors of \(\alpha\) and \(Y\) are equal to \(\hat\alpha\) and \(X\hat\beta + Z\hat\alpha\).

4.2.4 Example: Fitting a linear mixed model to Loblolly pines data

The data set “Loblolly” included in the nlme package contains longitudinal measurements of tree height for 14 Loblolly pine trees at 6 age points.

A plot of age by height for all trees suggests a common concave polynomial behavior—not quite linear.

library(nlme)
library(ggplot2)
head(Loblolly)

## Grouped Data: height ~ age | Seed
##    height age Seed
## 1    4.51   3  301
## 15  10.89   5  301
## 29  28.72  10  301
## 43  41.74  15  301
## 57  52.70  20  301
## 71  60.92  25  301

ggplot(data = Loblolly) + 
  geom_line(mapping = aes(x = age, y = height)) + 
  geom_point(mapping = aes(x = age, y = height)) + 
  facet_wrap(~ Seed, nrow = 2)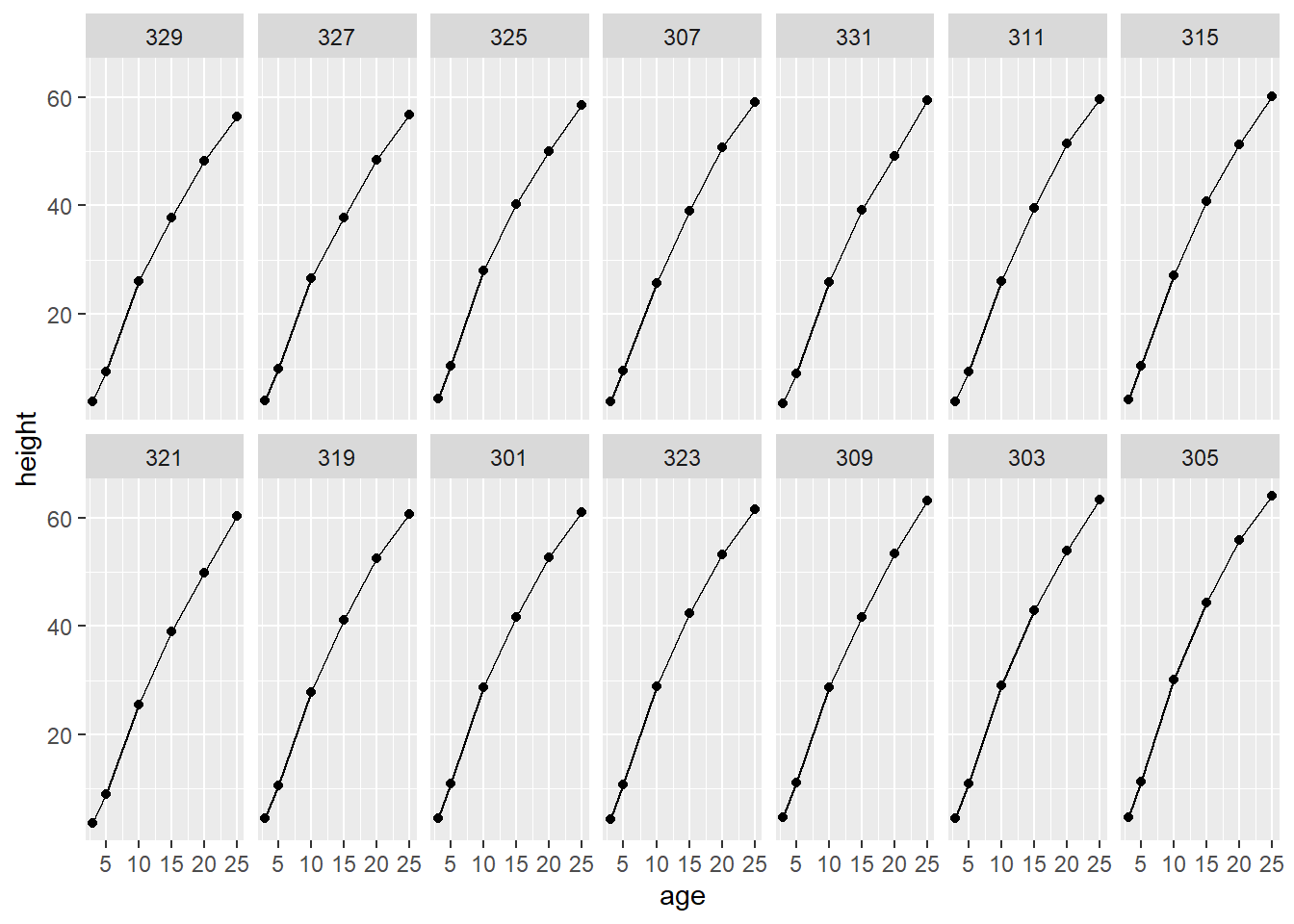

To model the mean height behavior we might choose a, say, third degree polynomial function of age. There are a few ways of doing this: specify a polynomial in age, a polynomial in {age - mean(age)}, or a basis of orthogonal polynomials. Both the second and third strategies are better than the first as coefficients of polynomial elements tend to be highly correlated unless those polynomial elements are orthogonal or the variable is centered.

We could model height as polynomial in age using only fixed effects. However, if we want to account for variation in those polynomials over trees we can introduce tree-specific effects. Those tree-specific effects could be fixed or random, and the choice depends on the sampling mechanism used to collect the data. If those specific trees are of interest and were sampled intentionally then fixed tree effects are appropriate. On the other hand, if the observed trees represent a random sample from a population of trees, then random tree effects are appropriate. It is also worth pointing out that, in most cases, many more degrees of freedom would be needed to estimate tree-specific fixed effects compared to tree-specific random effects. This polynomial mixed effects model looks like the following \[\begin{align*} Y_{ij} &= \beta_0 + \beta_1 X_{ij1}+ \beta_2 X_{ij2}+ \beta_3 X_{ij3}\\ &+ \beta_{i1} X_{ij1}+ \beta_{i2} X_{ij2}+ \beta_{i3} X_{ij3}\\ & + \epsilon_{ij} \end{align*}\] where \(i=1, \ldots, 14\) indexes trees, \(j = 1, \ldots, 6\) indexes ages, \(\beta_1\) through \(\beta_3\) are common coefficients for fixed polynomial age effects, and \(\beta_{i1}\) through \(\beta_{i3}\) are varying coefficients for age effects for each tree. The covariates \(X_{ij1}\) through \(X_{ij3}\) represent third degree orthogonal polynomials; i.e., they are not simply age, age\(^2\) and age\(^3\), more on those shortly. The random effects are normal with covariance \(\psi\), i.e., \((\beta_{i1},\beta_{i2},\beta_{i3})^\top \stackrel{iid}{\sim}N(0,\psi)\).

Since tree heights are recorded over time/ages it also makes sense to consider auto-correlated errors \(\epsilon_{i,j}\) with non-zero correlation over \(j\) within \(i\). For now, modeling these errors as zero-mean, time-dependent normal random variables with non-zero auto-correlation at lag 1, meaning \((\epsilon_{i,j}, \epsilon_{i,j+1})\) have non-zero correlation, so that \((\epsilon_{i1},\ldots, \epsilon_{i6})\stackrel{iid}{\sim} N(0,\Lambda)\) where \(\Lambda\) is positive definite and tri-diagonal.

Below we specify this model using the lme function from the nlme package. With default optimization specifications lme fails to fit this model, but lme converges if we simply increase the maximum number of iterations and function evaluations via the lmeControl function.

lmc <- lmeControl(niterEM=1000,msMaxIter=1000,msMaxEval=1000)

model1 <- lme(height ~ poly(age,3), data = Loblolly,
random = list(Seed = ~ poly(age,3)),
correlation = corAR1(form = ~ age|Seed), control = lmc)

summary(model1)

## Linear mixed-effects model fit by REML
##   Data: Loblolly 
##        AIC      BIC    logLik
##   242.2632 280.3756 -105.1316
## 
## Random effects:
##  Formula: ~poly(age, 3) | Seed
##  Structure: General positive-definite, Log-Cholesky parametrization
##               StdDev    Corr                
## (Intercept)   1.4302075 (Intr) p(,3)1 p(,3)2
## poly(age, 3)1 6.5811089  0.915              
## poly(age, 3)2 2.6961875 -0.812 -0.509       
## poly(age, 3)3 0.5943500 -0.125 -0.514 -0.477
## Residual      0.5906168                     
## 
## Correlation Structure: ARMA(1,0)
##  Formula: ~age | Seed 
##  Parameter estimate(s):
##          Phi1 
## -2.944641e-07 
## Fixed effects:  height ~ poly(age, 3) 
##                   Value Std.Error DF   t-value p-value
## (Intercept)    32.36440 0.3876331 67  83.49237   0.000
## poly(age, 3)1 186.44570 1.8553896 67 100.48870   0.000
## poly(age, 3)2 -21.84656 0.9317043 67 -23.44796   0.000
## poly(age, 3)3   0.05782 0.6116048 67   0.09454   0.925
##  Correlation: 
##               (Intr) p(,3)1 p(,3)2
## poly(age, 3)1  0.856              
## poly(age, 3)2 -0.619 -0.373       
## poly(age, 3)3 -0.032 -0.126 -0.096
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -1.84043424 -0.43798962 -0.03581482  0.69326329  1.56774981 
## 
## Number of Observations: 84
## Number of Groups: 14

While the summary function contains everything needed to determine if fixed effects are significant, it does not provide a straightforward explanation of all parameter estimates. With a little work, we can reproduce the estimated covariance parameters, and the estimated covariance of fixed effects. The getVarCov function provides the estimated covariance of the random effects nested within Seed; we could call these \(\hat\psi_i\) for seeds \(i=1, \ldots, 14\). The matrix \(\psi\) is block-diagonal, with identical blocks \(\psi_i\). The estimated residual variance is tri-diagonal with constant main diagonal elements \(\hat\sigma^2\) given by summary(model1)$sigma^2 and constant off-diagonal elements given by coef(model1$modelStruct$corStruct, unconstrained = FALSE).

The following helper function from the Matrix package can help in constructing the \(\Psi\) matrix:

bdiag_m <- function(lmat) {
    ## Copyright (C) 2016 Martin Maechler, ETH Zurich
    if(!length(lmat)) return(new("dgCMatrix"))
    stopifnot(is.list(lmat), is.matrix(lmat[[1]]),
              (k <- (d <- dim(lmat[[1]]))[1]) == d[2], # k x k
              all(vapply(lmat, dim, integer(2)) == k)) # all of them
    N <- length(lmat)
    if(N * k > .Machine$integer.max)
        stop("resulting matrix too large; would be  M x M, with M=", N*k)
    M <- as.integer(N * k)
    ## result: an   M x M  matrix
    new("dgCMatrix", Dim = c(M,M),
        ## 'i :' maybe there's a faster way (w/o matrix indexing), but elegant?
        i = as.vector(matrix(0L:(M-1L), nrow=k)[, rep(seq_len(N), each=k)]),
        p = k * 0L:M,
        x = as.double(unlist(lmat, recursive=FALSE, use.names=FALSE)))
}

We can match the standard errors and approximate p-values of the fixed effects using the following calculations (more on p-values later). One thing to mention: the \(Z\) design matrix of random effects seems not present in the lme object, and so we fit the same type of model using lmer from the lme4 package that more easily allows us to obtain this model matrix. We could have constructed this “by hand” but it has a large, block structure, and it’s just easier to extract from built-in functions.

library(lme4)

## Loading required package: Matrix

## 
## Attaching package: 'lme4'

## The following object is masked from 'package:nlme':
## 
##     lmList

model2lmer <- lmer(height ~ poly(age,3) + (poly(age,3) | Seed), data = Loblolly, control = lmerControl(optimizer="Nelder_Mead", optCtrl = list(maxfun = 100000), check.conv.grad = .makeCC("warning", tol = 0.71, relTol = NULL)))
Z <- model.matrix(model2lmer, type = 'random')
psi_i <- getVarCov(model1)
psi <- bdiag_m(list(psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i))
inv_psi <- solve(psi)
phi <- coef(model1$modelStruct$corStruct, unconstrained = FALSE)
L <- (summary(model1)$sigma^2)*diag(nrow(Loblolly))
for(i in 1:nrow(L)){
  for(j in nrow(L)){
    if(j==(i+1)||j==(i-1)){
      L[i,j] <- phi
    }
  }
}
invL <- solve(L)
A <- inv_psi+t(Z)%*%invL%*%Z
invA <- solve(A)
P<-invL-invL%*%Z%*%invA%*%t(Z)%*%invL
X <- model.matrix(model2lmer, type = 'fixed')
cov.beta.hat <- solve(t(X)%*%P%*%X)
Y <- Loblolly$height
beta.hat <- cov.beta.hat%*%t(X)%*%P%*%Y
beta.hat

## 4 x 1 Matrix of class "dgeMatrix"
##              [,1]
## [1,]  32.36440477
## [2,] 186.44569514
## [3,] -21.84656380
## [4,]   0.05781863

cov.beta.hat

## 4 x 4 Matrix of class "dgeMatrix"
##              [,1]       [,2]        [,3]         [,4]
## [1,]  0.150259390  0.6154960 -0.22367703 -0.007593674
## [2,]  0.615495986  3.4424706 -0.64470993 -0.143514475
## [3,] -0.223677034 -0.6447099  0.86807296 -0.054643528
## [4,] -0.007593673 -0.1435145 -0.05464352  0.374060450

beta.hat / sqrt(diag(cov.beta.hat)) # t-values

## 4 x 1 Matrix of class "dgeMatrix"
##              [,1]
## [1,]  83.49237468
## [2,] 100.48870309
## [3,] -23.44795779
## [4,]   0.09453594

1-pchisq(as.numeric((beta.hat / sqrt(diag(cov.beta.hat)))^2), 1) # rough p-values

## [1] 0.0000000 0.0000000 0.0000000 0.9246834

1-pf(as.numeric((beta.hat / sqrt(diag(cov.beta.hat)))^2), 1, nrow(Loblolly)-4)

## [1] 0.0000000 0.0000000 0.0000000 0.9249198

You may have noticed the estimated auto-regressive covariance term is essentially zero. This motivates us to fit a nested model in which this covariance term is zero, i.e., the residual covariance structure of \(\epsilon_i\), \(i=1, \ldots, n\) is simply iid with variance \(\sigma^2\).

model2 <- lme(height ~ poly(age,3), data = Loblolly,
random = list(Seed = ~ poly(age,3)),
correlation = NULL, control = lmc)

summary(model2)

## Linear mixed-effects model fit by REML
##   Data: Loblolly 
##        AIC      BIC    logLik
##   240.2632 275.9936 -105.1316
## 
## Random effects:
##  Formula: ~poly(age, 3) | Seed
##  Structure: General positive-definite, Log-Cholesky parametrization
##               StdDev    Corr                
## (Intercept)   1.4301995 (Intr) p(,3)1 p(,3)2
## poly(age, 3)1 6.5810089  0.915              
## poly(age, 3)2 2.6961948 -0.812 -0.509       
## poly(age, 3)3 0.5943572 -0.125 -0.514 -0.477
## Residual      0.5906184                     
## 
## Fixed effects:  height ~ poly(age, 3) 
##                   Value Std.Error DF   t-value p-value
## (Intercept)    32.36440 0.3876310 67  83.49282   0.000
## poly(age, 3)1 186.44570 1.8553648 67 100.49005   0.000
## poly(age, 3)2 -21.84656 0.9317069 67 -23.44789   0.000
## poly(age, 3)3   0.05782 0.6116069 67   0.09454   0.925
##  Correlation: 
##               (Intr) p(,3)1 p(,3)2
## poly(age, 3)1  0.856              
## poly(age, 3)2 -0.619 -0.373       
## poly(age, 3)3 -0.032 -0.126 -0.096
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -1.84042613 -0.43799912 -0.03581492  0.69325898  1.56775714 
## 
## Number of Observations: 84
## Number of Groups: 14

NLME is not the only package for fitting linear mixed models. LME4 is a newer package compared to NLME, and generally fits models much faster thanks to its better use of efficient linear algebra routines. However, LME4 is not as flexible as NLME when it comes to the available residual covariance structures one is able to fit. For example, LME4 does not have the flexibility to fit the AR(1) structure we fit for model1 above using the NLME package.

Below we fit model2 using LME4. The lmer model fitting function fails to fit the model with the default settings, much like the lme function from the NLME package. The main issue causing lack of convergence is a check function that evaluates the gradient of the likelihood at the final parameter estimates and requires it to be near zero. We have to violate this criteria in order to get the model to fit, which we can do by using the check.conv.grad argument of the control argument. Once we coerce lmer to converge using these options we see that it produces essentially the same estimates as lme with respect to model2.

library(lme4)
model2lmer <- lmer(height ~ poly(age,3) + (poly(age,3) | Seed), data = Loblolly, control = lmerControl(optimizer="Nelder_Mead", optCtrl = list(maxfun = 100000), check.conv.grad = .makeCC("warning", tol = 0.71, relTol = NULL)))
summary(model2lmer)

## Linear mixed model fit by REML ['lmerMod']
## Formula: height ~ poly(age, 3) + (poly(age, 3) | Seed)
##    Data: Loblolly
## Control: 
## lmerControl(optimizer = "Nelder_Mead", optCtrl = list(maxfun = 1e+05),  
##     check.conv.grad = .makeCC("warning", tol = 0.71, relTol = NULL))
## 
## REML criterion at convergence: 210.6
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.83857 -0.45408 -0.02587  0.65608  1.54812 
## 
## Random effects:
##  Groups   Name          Variance Std.Dev. Corr             
##  Seed     (Intercept)    1.9497  1.3963                    
##           poly(age, 3)1 40.8246  6.3894    0.91            
##           poly(age, 3)2  7.2430  2.6913   -0.82 -0.50      
##           poly(age, 3)3  0.6555  0.8096   -0.03 -0.37 -0.44
##  Residual                0.3506  0.5922                    
## Number of obs: 84, groups:  Seed, 14
## 
## Fixed effects:
##                Estimate Std. Error t value
## (Intercept)    32.36440    0.37873  85.455
## poly(age, 3)1 186.44570    1.80740 103.157
## poly(age, 3)2 -21.84656    0.93167 -23.449
## poly(age, 3)3   0.05782    0.63045   0.092
## 
## Correlation of Fixed Effects:
##             (Intr) p(,3)1 p(,3)2
## poly(ag,3)1  0.846              
## poly(ag,3)2 -0.621 -0.367       
## poly(ag,3)3 -0.011 -0.119 -0.117

Next, we will investigate various residual quantities to determine if our model assumptions are plausible.

4.3 Model diagnostics

As in pure fixed effects linear models, residuals are helpful for checking assumptions like linearity and normality. For mixed effects models, there are more ways to define residuals:

• Marginal residuals are the residuals formed by subtracting the fitted fixed effect from the response, that is, \(\hat e_{ij} := Y_{ij} - x_{ij}^\top \hat\beta\)

• Standardized marginal residuals remove the effect of correlation. The estimated covariance of \(\hat e\) is \(\hat\Sigma(\hat e) := \hat\Sigma - X(X^\top \hat\Sigma^{-1} X)^{-1}X^\top\). Let \(\hat\Sigma_i(\hat e)\) denote the fitted covariance of marginal residuals within group \(i\), and let \(\hat\Sigma_i(\hat e)^{-1/2}\) denote the lower Cholesky factor of \(\hat\Sigma_i(\hat e)^{-1}\). Then, \(\hat \epsilon_{i} = \hat\Sigma_i(\hat e)^{-1/2}\hat e_i\) denotes the vector of standardized marginal residuals for group \(i\).

• Conditional residuals also subtract the predicted random effect, \(\hat \xi_{ij} = Y_{ij} - x_{ij}^\top \hat\beta - z_{ij}^\top \hat \alpha\)

• Standardized conditional residuals \(\hat\phi_{ij}\) are formed by standardizing the conditional residuals by their estimated covariance, just as in the case of marginal residuals. The estimated covariance of conditional residuals is given by \[\hat\Sigma(\hat \phi) := (I-Z\hat A^{-1}Z^\top \hat\Lambda^{-1})\hat\Sigma(\hat e)(I-\hat\Lambda^{-1}Z\hat A^{-1}Z^\top).\]

A scatterplot of marginal residuals versus fixed covariates is useful for checking the assumption of linearity. Trends in this plot indicate an important omitted variable and/or nonlinearity.

Quantile-quantile plots of standardized marginal residuals within groups should match a standard normal distribution. If not, then the chosen within-group covariance structure is not good model for the given data. Comparing quantile-quantile plots for each group can be useful for assessing heteroskedasticity, although these comparisons become rough when groups have few individuals.

Large absolute standardized conditional residuals are indicate outliers. Plots of standardized conditional residuals versus the fitted values \(X\hat\beta + Z\hat\alpha\) may also reveal heteroskedasticity over/between groups—which would suggest modifying the structure of \(\Lambda\) if it is assumed to be \(\sigma^2 I_n\) as is common.

4.3.1 Model diagnostics for Loblolly pines data

We begin by plotting the amrginal residuals from the cubic model fit with LME4 which we called model2. The marginal residuals exhibit some pattern in age. This suggests fitting a higher-order polynomial model.

marginal.resids <- Loblolly$height - model.matrix(model2lmer, type = 'fixed')%*%fixef(model2lmer)
plot(Loblolly$age, marginal.resids, xlab = 'age', ylab = 'marginal residual')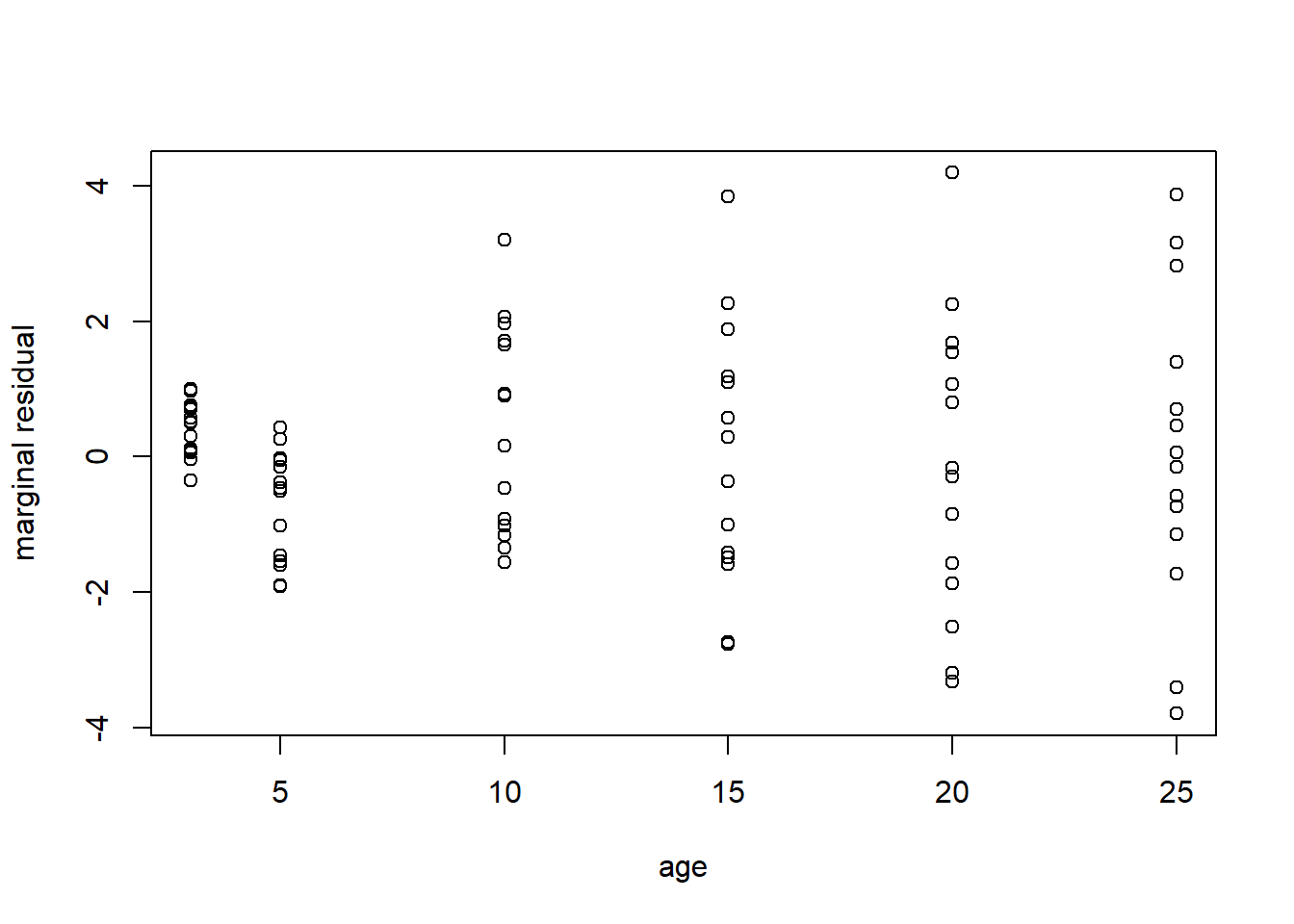

A 5th order polynomial appears to fit the data; however, we cannot include 5th order polynomial random effects, so we will need to make some choice on random effect structure by investigating standardized residuals.

library(lme4)
model3lmer <- lmer(height ~ poly(age,5) + (1 | Seed), data = Loblolly, control = lmerControl(optimizer="Nelder_Mead", optCtrl = list(maxfun = 100000), check.conv.grad = .makeCC("warning", tol = 0.71, relTol = NULL)))
marginal.resids3 <- Loblolly$height - model.matrix(model3lmer, type = 'fixed')%*%fixef(model3lmer)
plot(Loblolly$age, marginal.resids3, xlab = 'age', ylab = 'marginal residual')

Above we fit a 5th-order polynomial model with only random intercepts by Seed/tree. This means that each tree’s age-height relationship is simply a shifted (up or down) version of the same polynomial. Based on our BLUPs, plotted below, the random effects do not seem sufficiently flexible to model trees 329, 327, and 305, for example. It certainly looks like we need to add random polynomial effects.

Loblolly$fitted3 <- fitted(model3lmer)

ggplot(data = Loblolly) + 
  geom_line(mapping = aes(x = age, y = height)) + 
  geom_point(mapping = aes(x = age, y = height)) + 
  geom_point(mapping = aes(x = age, y = fitted3, color = 'red')) +
  facet_wrap(~ Seed, nrow = 2)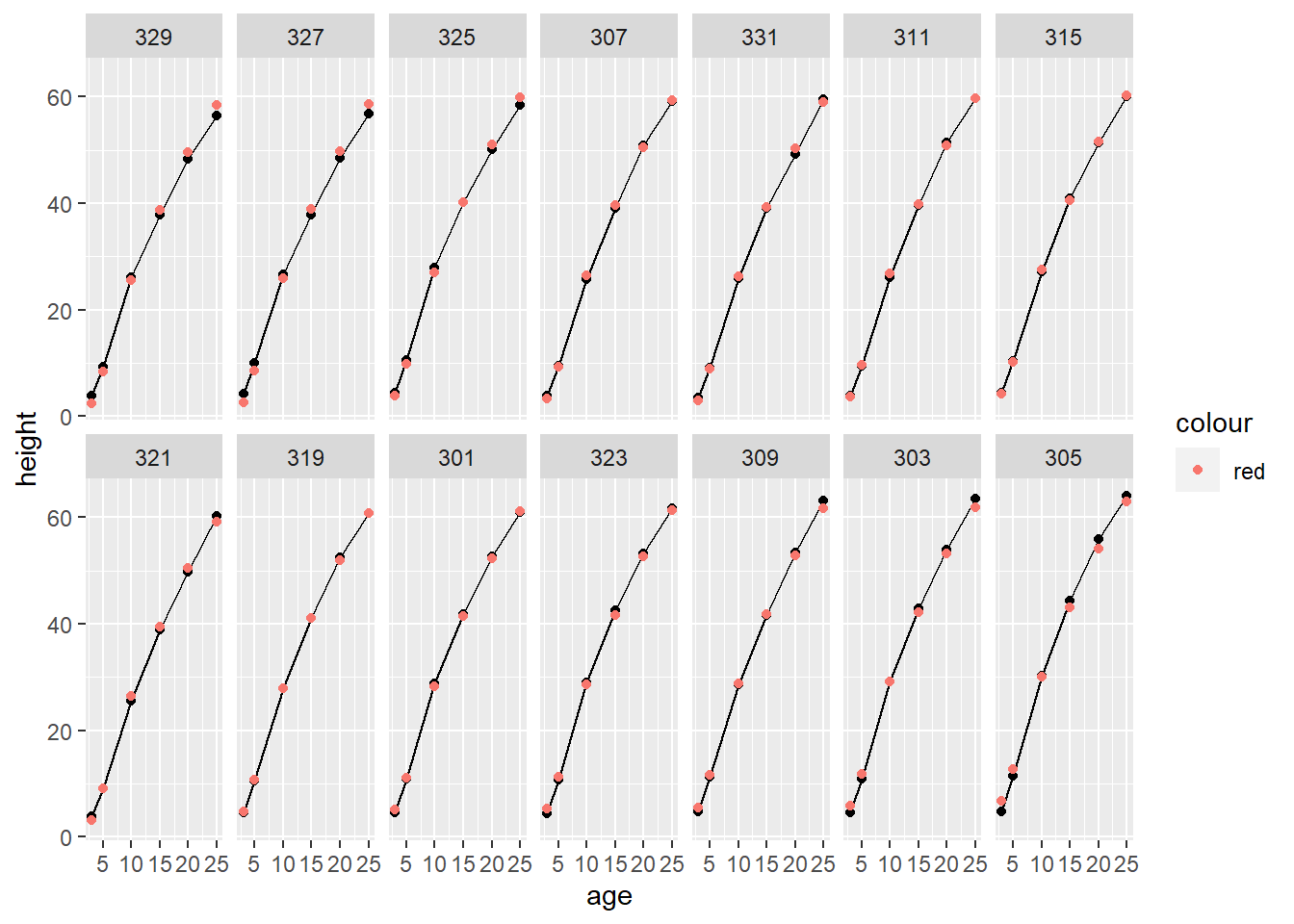

Taking those poorly-fitting BLUPs into account, we fit a model with quadratic random effects. Our predictions look much more accurate after including these additional random effects.

model4lmer <- lmer(height ~ poly(age,5) + (poly(age,2) | Seed), data = Loblolly)
marginal.resids4 <- Loblolly$height - model.matrix(model4lmer, type = 'fixed')%*%fixef(model4lmer)
Loblolly$fitted4 <- fitted(model4lmer)
ggplot(data = Loblolly) + 
  geom_line(mapping = aes(x = age, y = height)) + 
  geom_point(mapping = aes(x = age, y = height)) + 
  geom_point(mapping = aes(x = age, y = fitted4, color = 'red')) +
  facet_wrap(~ Seed, nrow = 2)

The following calculations produce standardized marginal residuals, which we can investigate for normality and the overall appropriateness of the within tree covariance structure.

Z <- model.matrix(model4lmer, type = 'random')
dim_cov <- dim(attr(VarCorr(model4lmer)[1]$Seed, 'correlation'))[1]
psi_i <- as.matrix(VarCorr(model4lmer)[1]$Seed[1:dim_cov,1:dim_cov])
psi <- bdiag_m(list(psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i,psi_i))
inv_psi <- solve(psi)
L <- (summary(model4lmer)$sigma^2)*diag(nrow(Loblolly))
invL <- solve(L)
A <- inv_psi+t(Z)%*%invL%*%Z
invA <- solve(A)
P<-invL-invL%*%Z%*%invA%*%t(Z)%*%invL
X <- as.matrix(model.matrix(model4lmer, type = 'fixed'))
cov.beta.hat <- solve(t(X)%*%P%*%X)
Sigma_e <- P-X%*%cov.beta.hat%*%t(X)
Y <- Loblolly$height
beta.hat <- cov.beta.hat%*%t(X)%*%P%*%Y
Pi <- as.matrix(P)[1:6,1:6]
cholPi <- t(solve(chol(solve(Pi))))
standardized_resids <- rep(NA,84)
seed=1
cov.check <- 0
for(i in 1:14){
  standardized_resids[(seed-1)*6+(1:6)] <- t(cholPi)%*%marginal.resids4[(seed-1)*6+(1:6)]
  cov.check <- cov.check + sum((diag(6)-standardized_resids[(seed-1)*6+(1:6)]%*%t(standardized_resids[(seed-1)*6+(1:6)]))^2)
  seed <- seed + 1
}

Loblolly$standardized_resids <- standardized_resids

Below we view boxplots of standardized marginal residuals by tree, sorting by least to greatest variability. As a sanity check we also produce a reference plot of 14 boxplots of 6 standard normal random variates each. This plot serves as a visual inspection to check whether or not the standardized marginal residuals appear to behave as realizations of standard normal random variables. There is slightly more variability in our standardized marginal residuals than in the exact standard normal samples, probably due mostly to a few poorly fitting observations, but nothing that causes us concern.

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ tibble  3.1.8      ✔ dplyr   1.0.10
## ✔ tidyr   1.2.1      ✔ stringr 1.4.1 
## ✔ readr   2.1.2      ✔ forcats 0.5.2 
## ✔ purrr   0.3.4      
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::collapse() masks nlme::collapse()
## ✖ tidyr::expand()   masks Matrix::expand()
## ✖ dplyr::filter()   masks stats::filter()
## ✖ dplyr::lag()      masks stats::lag()
## ✖ tidyr::pack()     masks Matrix::pack()
## ✖ tidyr::unpack()   masks Matrix::unpack()

Loblolly<-Loblolly %>% 
  group_by(Seed) %>% 
  mutate(sd_stan_resids = sd(standardized_resids)) %>% 
  arrange(sd_stan_resids) %>%
  ungroup()

Loblolly$Seed <- factor(Loblolly$Seed, ordered = FALSE, levels = unique(Loblolly$Seed))

plot(Loblolly$Seed, Loblolly$standardized_resids, xlab = 'Seed', ylab = 'standardized marginal residual', ylim = c(-6,6))

fakedata <- cbind(rnorm(84), c(rep(1,6),rep(2,6),rep(3,6),rep(4,6),
                                rep(5,6),rep(6,6),rep(7,6),rep(8,6),
                                rep(9,6),rep(10,6),rep(11,6),rep(12,6),
                                rep(13,6),rep(14,6)))

fakedata <- data.frame(fakedata)

fakedata<-fakedata %>% 
  group_by(X2) %>% 
  mutate(sd_X1 = sd(X1)) %>% 
  arrange(sd_X1) %>%
  ungroup()

fakedata$X2 <- factor(fakedata$X2, ordered = FALSE, levels = unique(fakedata$X2))

plot(fakedata$X2, fakedata$X1, xlab = 'random normals', ylab = 'sample standard deviation', ylim = c(-6,6))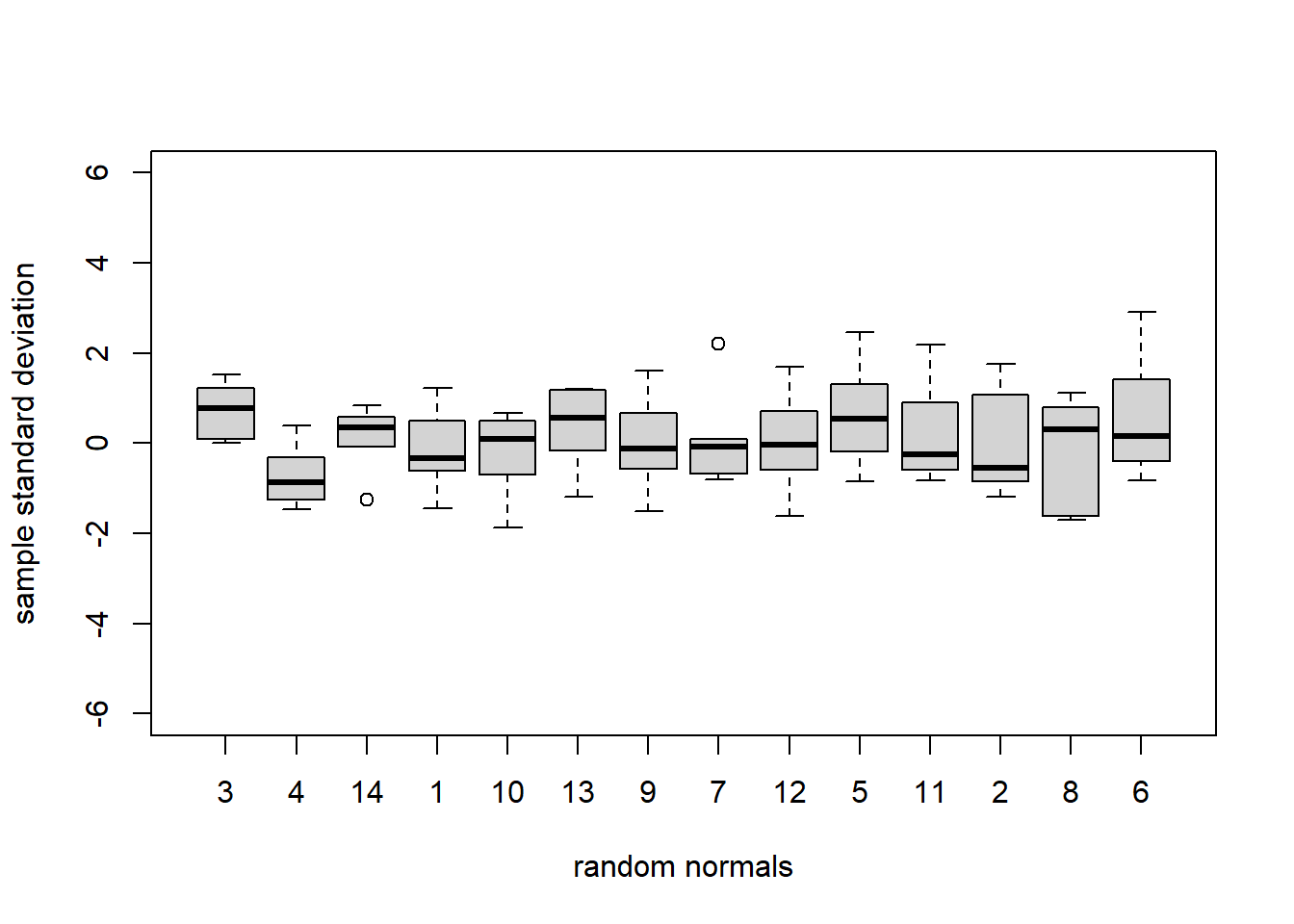

We also compute standardized conditional residuals and compare them to a standard normal distribution. A qq-plot suggests a reasonable match and the Shapiro-Wilk test for normality does not reject the supposition these residuals are standard normal. There does not seem to be substantial heteroskedasticity by age or tree that would suggest we modify our model for the covariance structure.

model4lmer <- lmer(height ~ poly(age,5) + (poly(age,2) | Seed), data = Loblolly)
B <- (diag(nrow(Loblolly)) - Z%*%invA%*%t(Z)%*%invL)
P2 <- B%*%solve(P)%*%t(B)
cholP2 <- t(solve(chol(P2)))
standardized_conditional_residuals <- cholP2%*%(Loblolly$height - fitted(model4lmer))
qqnorm(standardized_conditional_residuals)
qqline(standardized_conditional_residuals)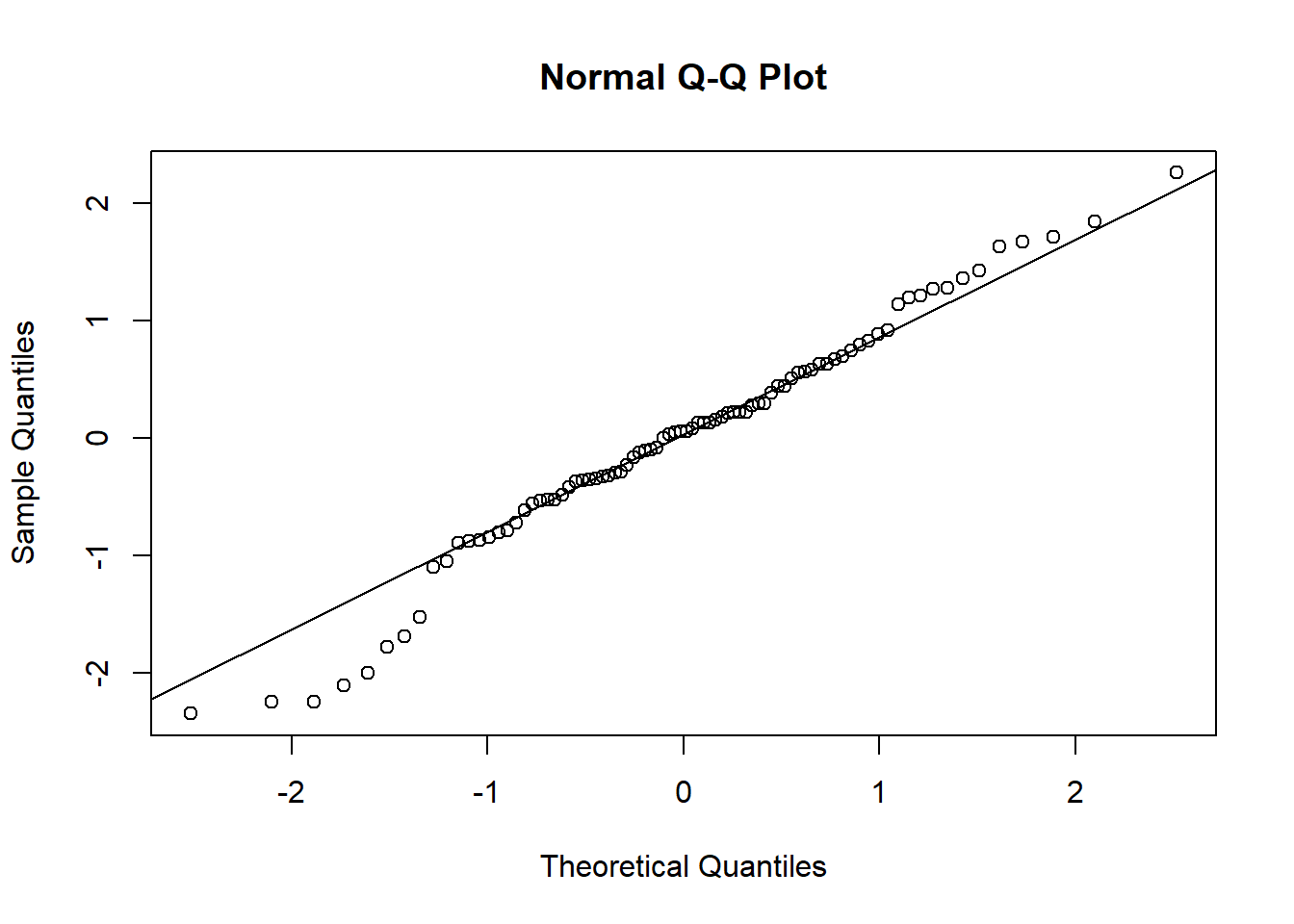

shapiro.test(as.numeric(standardized_conditional_residuals))

## 
##  Shapiro-Wilk normality test
## 
## data:  as.numeric(standardized_conditional_residuals)
## W = 0.97853, p-value = 0.1735

Loblolly$standardized_conditional_residuals <- as.numeric(standardized_conditional_residuals)
boxplot(standardized_conditional_residuals~Seed, data = Loblolly,xlab = 'Seed', ylab = 'standardized conditional residual', ylim = c(-3,3))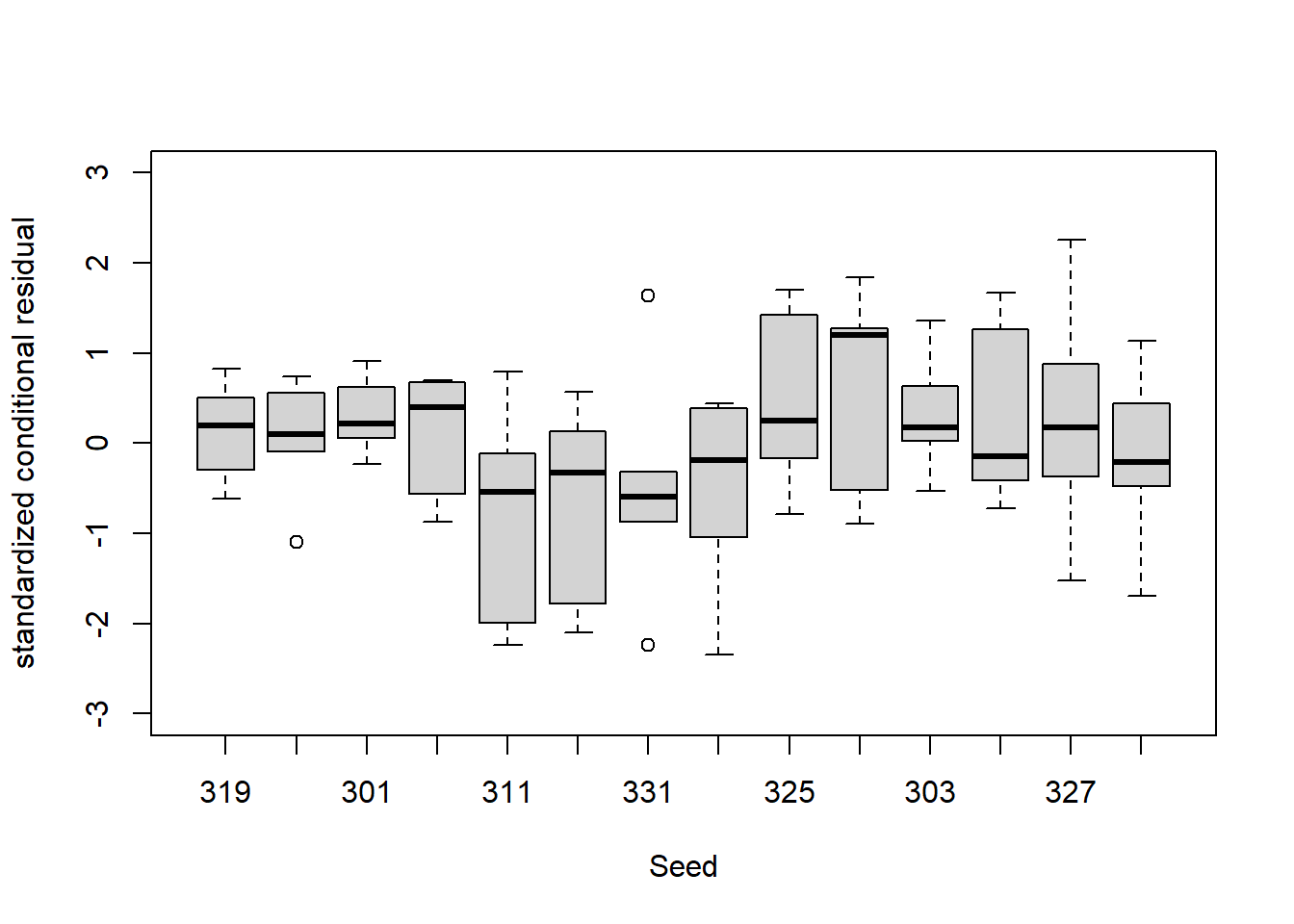

boxplot(standardized_conditional_residuals~age, data = Loblolly)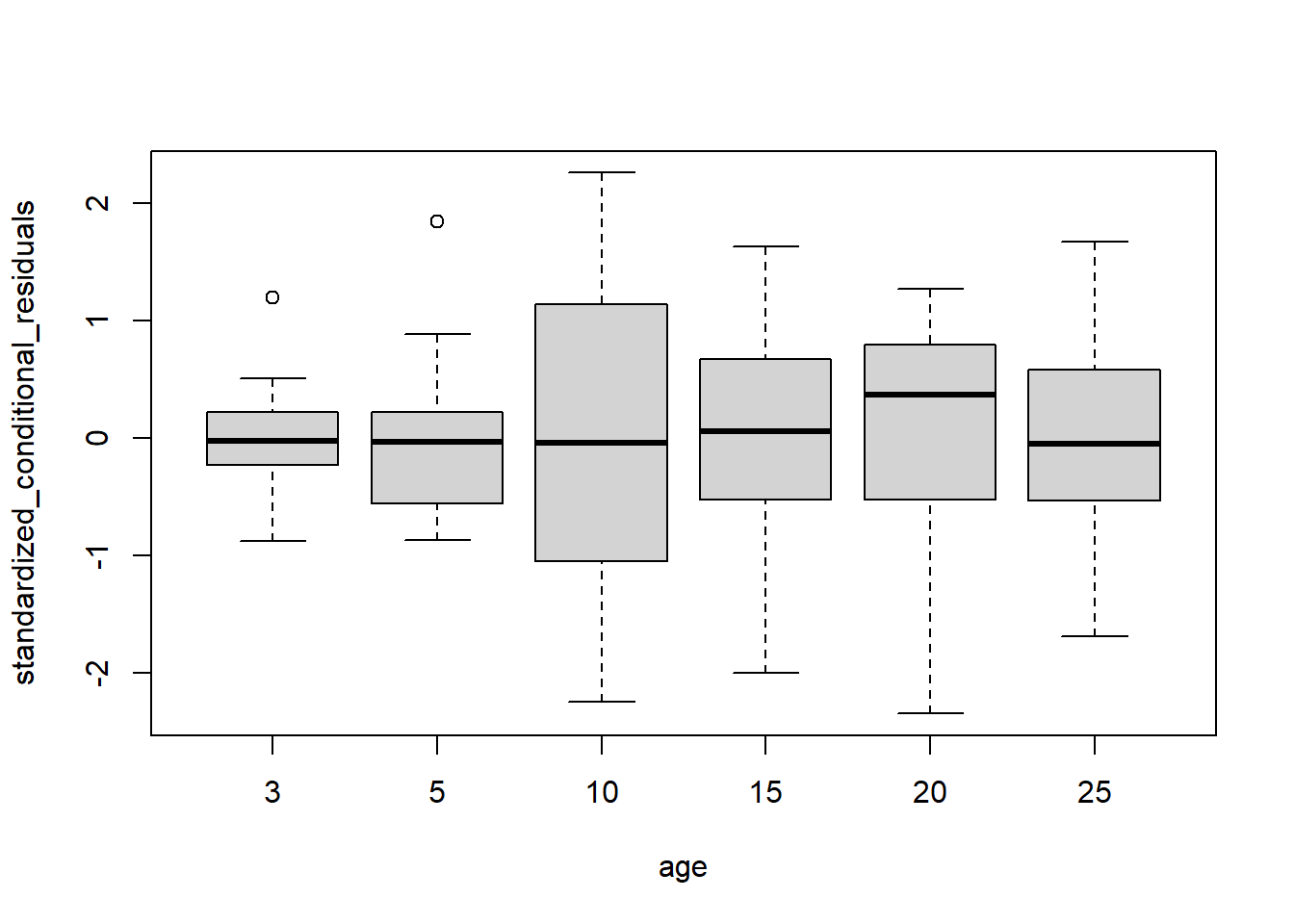

Content with the fit of our model, we will next discuss inference for fixed effects and model comparisons.

4.4 Inference for fixed effects, random effects, and model comparisons

The most common inferential questions concern the regression coefficient vector \(\beta\). Wald confidence regions for \(\beta\) are defined by the sets \[C_\alpha := \{b: (b - \hat\beta)(X^\top V^{-1}X)^{-1}(b - \hat\beta)<\chi^2_{1-\alpha, p}\}\] where \(\chi^2_{1-\alpha, p}\) is the upper \(\alpha\) quantile of the Chi-squared distribution with \(p\) degrees of freedom. Unfortunately, these regions are only exact when \(\theta\) is known and can severely undercover for small sample sizes. Software packages typically perform an adjustment, such as the Kenward-Rogers scaling, which is a generalization of Satterthwaite’s approximation.

For a point null hypothesis \(H_0: \beta = \beta_{0}\) the Wald test statistic is \[W = (\beta_0 - \hat\beta)(X^\top V^{-1}X)^{-1}(\beta_0 - \hat\beta)\] and \(H_0\) is rejected if \(W > \chi^2_{1-\alpha, p}\). More generally, let \(D\) denote an \(r\times p\) matrix \(r<p\) of full rank. Reject the null hypothesis \(H_0:D\beta = b_0\) if \(W > \chi^2_{1-\alpha, r}\) where \[W = (b_0 - D\hat\beta)(D X^\top V^{-1}X D^\top)^{-1}(b_0 - D\hat\beta)\]

(Generalized) Likelihood ratio tests may be used to compare nested models. Model A is nested in B if A may be written as B with some of B’s parameters equal to zero, provided zero is not a boundary value for the parameter being omitted in model A. For example, A is nested in B if A contains only a subset of B’s fixed effects, a subset of B’s random effects, a nested residual covariance structure like iid versus AR(1) as in the above example, or a combination of these three. When likelihood ratio tests are performed to compare nested models with different fixed effects both models should be fit using maximum likelihood rather than REML because residual likelihoods for two different sets of fixed effects are not comparable.

An example of models that are not nested is the cubic model above called model1 versus a model with linear, quadratic and fourth order fixed effects but no third order fixed effect. AIC and/or BIC comparisons (based on the full likelihoods) are useful for comparing non-nested models (remember: lower AIC/BIC is better).

As mentioned previously, in the context of linear mixed models, test statistics rarely have exact Chi-squared or F null distributions—the exceptions pertain to balanced experiments. In fact, these approximations may be very rough, depending on the model and sample sizes. For this reason, the LMER package does not even report p-values at this time. But, there are a few options for producing fairly reliable p-values. One option is to utilize the lmerTest package which provides functions for testing fixed effects using Satterthwaite or Kenward-Rogers corrected null distributions. Another option is to use the parametric bootstrap (based on sampling a multivariate normal distribution) to provide bootstrap-based tests and confidence intervals. The bootstrap method is endorsed by the creators of LME4, and they have included the bootMer function in that package to facilitate bootstrap-based inference in linear mixed models.

4.4.1 Inference on fixed effects for Loblolly pines data

The first question of interest, which we hinted at before, is whether or not we need to model the residual error as having a time-dependent, e.g., AR(1), structure. Recall our point estimate for the auto-regressive correlation was essentially zero, suggesting it played no role in the model fit. The NLME package contains an anova method for comparing models. While we should get into the habit of comparing models fit by maximum likelihood, it makes little difference if we use REML for this comparison because the models only differ in covariance structure, not fixed-effects structure. Whether we compare models fit by REML or ML, we see overwhelming evidence that the simpler model, the one without an auto-regressive error structure, is just as good as the more complicated model.

anova(model1, model2)

##        Model df      AIC      BIC    logLik   Test      L.Ratio p-value
## model1     1 16 242.2632 280.3756 -105.1316                            
## model2     2 15 240.2632 275.9936 -105.1316 1 vs 2 7.727313e-06  0.9978

model2ml <- lme(height ~ poly(age,3), data = Loblolly,
random = list(Seed = ~ poly(age,2)),
correlation = NULL, control = lmc, method = 'ML')
summary(model2ml)

## Linear mixed-effects model fit by maximum likelihood
##   Data: Loblolly 
##       AIC     BIC    logLik
##   236.479 263.218 -107.2395
## 
## Random effects:
##  Formula: ~poly(age, 2) | Seed
##  Structure: General positive-definite, Log-Cholesky parametrization
##               StdDev    Corr         
## (Intercept)   1.3770489 (Intr) p(,2)1
## poly(age, 2)1 6.3146599  0.920       
## poly(age, 2)2 2.5921354 -0.812 -0.519
## Residual      0.5862648              
## 
## Fixed effects:  height ~ poly(age, 3) 
##                   Value Std.Error DF   t-value p-value
## (Intercept)    32.36440 0.3827742 67  84.55220  0.0000
## poly(age, 3)1 186.44570 1.8307134 67 101.84319  0.0000
## poly(age, 3)2 -21.84656 0.9299619 67 -23.49189  0.0000
## poly(age, 3)3   0.05782 0.6007426 67   0.09625  0.9236
##  Correlation: 
##               (Intr) p(,3)1 p(,3)2
## poly(age, 3)1  0.856              
## poly(age, 3)2 -0.611 -0.374       
## poly(age, 3)3  0.000  0.000  0.000
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -1.88150210 -0.48683940 -0.08576157  0.70311783  1.80653065 
## 
## Number of Observations: 84
## Number of Groups: 14

model1ml <- lme(height ~ poly(age,3), data = Loblolly,
random = list(Seed = ~ poly(age,2)),
correlation = corAR1(form = ~ age|Seed), control = lmc, method = 'ML')

summary(model1ml)

## Linear mixed-effects model fit by maximum likelihood
##   Data: Loblolly 
##       AIC      BIC    logLik
##   238.479 267.6488 -107.2395
## 
## Random effects:
##  Formula: ~poly(age, 2) | Seed
##  Structure: General positive-definite, Log-Cholesky parametrization
##               StdDev    Corr         
## (Intercept)   1.3770407 (Intr) p(,2)1
## poly(age, 2)1 6.3146152  0.920       
## poly(age, 2)2 2.5921670 -0.812 -0.519
## Residual      0.5862659              
## 
## Correlation Structure: ARMA(1,0)
##  Formula: ~age | Seed 
##  Parameter estimate(s):
##          Phi1 
## -7.729034e-07 
## Fixed effects:  height ~ poly(age, 3) 
##                   Value Std.Error DF   t-value p-value
## (Intercept)    32.36440 0.3827720 67  84.55269  0.0000
## poly(age, 3)1 186.44570 1.8307022 67 101.84382  0.0000
## poly(age, 3)2 -21.84656 0.9299693 67 -23.49171  0.0000
## poly(age, 3)3   0.05782 0.6007438 67   0.09625  0.9236
##  Correlation: 
##               (Intr) p(,3)1 p(,3)2
## poly(age, 3)1  0.856              
## poly(age, 3)2 -0.611 -0.374       
## poly(age, 3)3  0.000  0.000  0.000
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -1.88152563 -0.48682881 -0.08576799  0.70309957  1.80652460 
## 
## Number of Observations: 84
## Number of Groups: 14

anova(model1ml, model2ml)

##          Model df     AIC      BIC    logLik   Test      L.Ratio p-value
## model1ml     1 12 238.479 267.6488 -107.2395                            
## model2ml     2 11 236.479 263.2180 -107.2395 1 vs 2 4.513881e-07  0.9995

Next we investigate whether a degree 5 or 4 polynomial is enough to model the age-height relationship. Using lmerTest we can produce corrected p-values for each fixed effect within model2—the model with an iid residual error structure. It’s clear that the cubic term provides no benefit, so we omit it and fit model3. An anova method is also included with lmer, and notice that lmer automatically recognizes we want to compare nested models with differing fixed effects and refits those models by ML—how delightful. this time, the more complex 5th degree polynomial model is clearly preferred.

summary(model2lmer)

## Linear mixed model fit by REML ['lmerMod']
## Formula: height ~ poly(age, 3) + (poly(age, 3) | Seed)
##    Data: Loblolly
## Control: 
## lmerControl(optimizer = "Nelder_Mead", optCtrl = list(maxfun = 1e+05),  
##     check.conv.grad = .makeCC("warning", tol = 0.71, relTol = NULL))
## 
## REML criterion at convergence: 210.6
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.83857 -0.45408 -0.02587  0.65608  1.54812 
## 
## Random effects:
##  Groups   Name          Variance Std.Dev. Corr             
##  Seed     (Intercept)    1.9497  1.3963                    
##           poly(age, 3)1 40.8246  6.3894    0.91            
##           poly(age, 3)2  7.2430  2.6913   -0.82 -0.50      
##           poly(age, 3)3  0.6555  0.8096   -0.03 -0.37 -0.44
##  Residual                0.3506  0.5922                    
## Number of obs: 84, groups:  Seed, 14
## 
## Fixed effects:
##                Estimate Std. Error t value
## (Intercept)    32.36440    0.37873  85.455
## poly(age, 3)1 186.44570    1.80740 103.157
## poly(age, 3)2 -21.84656    0.93167 -23.449
## poly(age, 3)3   0.05782    0.63045   0.092
## 
## Correlation of Fixed Effects:
##             (Intr) p(,3)1 p(,3)2
## poly(ag,3)1  0.846              
## poly(ag,3)2 -0.621 -0.367       
## poly(ag,3)3 -0.011 -0.119 -0.117

library(lmerTest)

## Warning: package 'lmerTest' was built under R version 4.2.2

## 
## Attaching package: 'lmerTest'

## The following object is masked from 'package:lme4':
## 
##     lmer

## The following object is masked from 'package:stats':
## 
##     step

X5 <- poly(Loblolly$age,5)
Loblolly_poly <- Loblolly
Loblolly_poly$linear <- X5[,1]
Loblolly_poly$quadratic <- X5[,2]
Loblolly_poly$cubic <- X5[,3]
Loblolly_poly$quartic <- X5[,4]
Loblolly_poly$quintic <- X5[,5]
model2lmer_quartic <- lmer(height ~ linear+quadratic+cubic+quartic + (linear+quadratic | Seed), data = Loblolly_poly)
summary(model2lmer_quartic)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: height ~ linear + quadratic + cubic + quartic + (linear + quadratic |  
##     Seed)
##    Data: Loblolly_poly
## 
## REML criterion at convergence: 189.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -1.7644 -0.5447 -0.1186  0.5125  1.9876 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr       
##  Seed     (Intercept)  2.0589  1.4349              
##           linear      44.2363  6.6510    0.91      
##           quadratic    7.8677  2.8050   -0.79 -0.45
##  Residual              0.2462  0.4962              
## Number of obs: 84, groups:  Seed, 14
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)  32.36440    0.38729  13.01326  83.567  < 2e-16 ***
## linear      186.44570    1.84552  13.03103 101.026  < 2e-16 ***
## quadratic   -21.84656    0.89900  13.78421 -24.301 1.03e-12 ***
## cubic         0.05782    0.49620  52.99715   0.117    0.908    
## quartic       2.48987    0.49620  52.99715   5.018 6.24e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) linear qudrtc cubic 
## linear     0.864                     
## quadratic -0.651 -0.364              
## cubic      0.000  0.000  0.000       
## quartic    0.000  0.000  0.000  0.000

model2lmer_quintic <- lmer(height ~ linear+quadratic+cubic+quartic+quintic + (linear+quadratic | Seed), data = Loblolly_poly)
summary(model2lmer_quintic)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: height ~ linear + quadratic + cubic + quartic + quintic + (linear +  
##     quadratic | Seed)
##    Data: Loblolly_poly
## 
## REML criterion at convergence: 148.7
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.90907 -0.43377 -0.01942  0.44241  2.29016 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr       
##  Seed     (Intercept)  2.0794  1.4420              
##           linear      45.6633  6.7575    0.89      
##           quadratic    8.5419  2.9227   -0.77 -0.39
##  Residual              0.1153  0.3395              
## Number of obs: 84, groups:  Seed, 14
## 
## Fixed effects:
##              Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)  32.36440    0.38717  12.99880  83.593  < 2e-16 ***
## linear      186.44570    1.83765  13.00055 101.459  < 2e-16 ***
## quadratic   -21.84656    0.85172  13.12063 -25.650 1.34e-12 ***
## cubic         0.05782    0.33955  52.00132   0.170    0.865    
## quartic       2.48987    0.33955  52.00132   7.333 1.46e-09 ***
## quintic      -2.65565    0.33955  52.00132  -7.821 2.44e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##           (Intr) linear qudrtc cubic  quartc
## linear     0.872                            
## quadratic -0.700 -0.354                     
## cubic      0.000  0.000  0.000              
## quartic    0.000  0.000  0.000  0.000       
## quintic    0.000  0.000  0.000  0.000  0.000

anova(model2lmer_quartic, type = 'III', ddf = 'Ken')

## Type III Analysis of Variance Table with Kenward-Roger's method
##           Sum Sq Mean Sq NumDF DenDF    F value    Pr(>F)    
## linear    2513.0  2513.0     1    13 10206.2419 < 2.2e-16 ***
## quadratic  145.4   145.4     1    13   590.5368 3.212e-12 ***
## cubic        0.0     0.0     1    40     0.0136    0.9078    
## quartic      6.2     6.2     1    40    25.1786 1.119e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

anova(model2lmer_quintic, type = 'III', ddf = 'Ken')

## Type III Analysis of Variance Table with Kenward-Roger's method
##            Sum Sq Mean Sq NumDF DenDF   F value    Pr(>F)    
## linear    1186.82 1186.82     1    13 10293.880 < 2.2e-16 ***
## quadratic   75.85   75.85     1    13   657.916 1.613e-12 ***
## cubic        0.00    0.00     1    39     0.029    0.8657    
## quartic      6.20    6.20     1    39    53.771 7.514e-09 ***
## quintic      7.05    7.05     1    39    61.170 1.643e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

anova(model2lmer_quartic, model2lmer_quintic)

## refitting model(s) with ML (instead of REML)

## Data: Loblolly_poly
## Models:
## model2lmer_quartic: height ~ linear + quadratic + cubic + quartic + (linear + quadratic | Seed)
## model2lmer_quintic: height ~ linear + quadratic + cubic + quartic + quintic + (linear + quadratic | Seed)
##                    npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## model2lmer_quartic   12 216.71 245.88 -96.355   192.71                         
## model2lmer_quintic   13 175.16 206.76 -74.581   149.16 43.547  1  4.139e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

As an alternative to Chi-squared/F-based tests performed using NLME or lmerTest, we provide a bootstrap-based analysis using bootMer. The downside of bootMer is that it is slow due to the need to refit the linear mixed model for each bootstrap simulation. Below we perform 100 such bootstrap simulations of model2—which is not enough for precise answers—but it is enough to get a good idea that the cubic term is ignorable and that the other fixed effects are significant.

fun <- function(model) summary(model)$coefficients[,1]
booted <- bootMer(model2lmer_quintic, fun, 100, type = 'parametric')

library(boot)
boot.ci(booted, conf = 0.95, type = 'basic', index = 1)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 100 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = booted, conf = 0.95, type = "basic", index = 1)
## 
## Intervals : 
## Level      Basic         
## 95%   (31.62, 33.25 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable

boot.ci(booted, conf = 0.95, type = 'basic', index = 2)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 100 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = booted, conf = 0.95, type = "basic", index = 2)
## 
## Intervals : 
## Level      Basic         
## 95%   (182.9, 190.8 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable

boot.ci(booted, conf = 0.95, type = 'basic', index = 3)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 100 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = booted, conf = 0.95, type = "basic", index = 3)
## 
## Intervals : 
## Level      Basic         
## 95%   (-23.67, -20.05 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable

boot.ci(booted, conf = 0.95, type = 'basic', index = 4)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 100 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = booted, conf = 0.95, type = "basic", index = 4)
## 
## Intervals : 
## Level      Basic         
## 95%   (-0.6187,  0.7864 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable

boot.ci(booted, conf = 0.95, type = 'basic', index = 5)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 100 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = booted, conf = 0.95, type = "basic", index = 5)
## 
## Intervals : 
## Level      Basic         
## 95%   ( 1.795,  3.169 )  
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable